LearnOpenGL(08) - 카메라

이전글: LearnOpenGL(07) - 좌표계

다음글:

Camera

지난 장에서 뷰 행렬과 뷰 행렬을 이용해 어떻게 씬에서 이동할지 이야기 했습니다(뒤쪽으로 약간 이동했었죠). OpenGL은 카메라라는 컨셉에 친묵하지 않습니다. 하지만 씬의 모든 오브젝트를 반대 방향으로 움직여 우리가 움직이는 것처럼 보이도록은 할 수 있습니다.

이번 장에서는 OpenGL에서 어떻게 카메라를 설정하고, 어떻게 3D 씬에서 자유롭게 돌아다닐지 이야기해 보겠습니다. 또한 키보드와 마우스 입력에 대해서도 다루고 커스텀 카메라 클래스로 마무리 하겠습니다.

Camera/View space

카메라/뷰 공간에 대해서 얘기하는 건 씬의 원점으로서의 카메라의 시점으로 본 버텍스 좌표에 대해 말하는 것입니다: 뷰 매트릭스는 모든 월드 좌표를 카메라의 위치와 방향에 상대적인 뷰 좌표로 변환합니다. 카메라를 정의하려면 월드 공간에서의 위치, 보고 있는 방향, 카메라에서 오른쪽과 위쪽을 가르키는 벡터들이 필요합니다. 주의 깊게 읽어 보신 분들은 우리가 카메라를 원점으로 하여 서로 수직인 3개의 단위 축으로 좌표계를 생성하려는 것을 알아채셨을 겁니다.

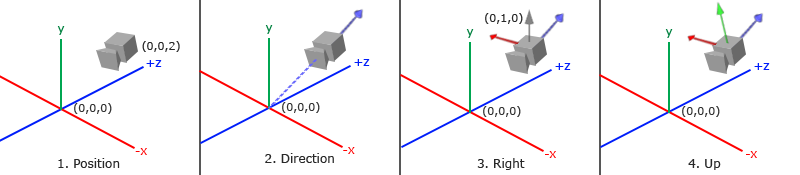
1. Camera position

카메라 위치를 알아내는 건 간단합니다. 카메라의 위치는 월드 공간에서 카메라를 향하는 벡터입니다. 지난 장에서 우리는 카메라를 다음과 같은 위치에 뒀습니다:

glm::vec3 cameraPos = glm::vec3(0.0f, 0.0f, 3.0f);

양의 z축이 사용자를 향한다는 것을 잊지마세요, 카메라를 뒤로 움직이고 싶다면 양의 z축으로 움직이면 됩니다.

2. Camera direction

다음으로 필요한 것은 카메라가 가리키는 방향입니다. 지금은 카메라가 씬의 원점인 (0, 0, 0)을 가리키도록 합시다.  두 벡터를 서로 빼면 두 벡터의 차이만큼의 벡터를 얻는다는 것을 기억하나요?(번역이 이상한데 아마 벡터A에서 벡터B를 빼면 B에서 A로 가는 벡터가 나온다는 얘기 같습니다.) 따라서 씬의 원점 벡터에서 카메라 위치 벡터를 빼면 원하는 방향 벡터를 얻게 됩니다. 뷰 행렬 좌표계대해 카메라의 z축이 양수이기를 바라고 관례에 따라(OpenGL)에서 카메라가 음의 z축을 가리키기 때문에 방향 벡터를 무효화하려고 합니다. 빼기 순서를 바꾸면 카메라의 양의 z축을 가리키는 벡터를 얻습니다.

glm::vec3 cameraTarget = glm::vec3(0.0f, 0.0f, 0.0f);
glm::vec3 cameraDirection = glm::normalize(cameraPos - cameraTarget);

3. Right axis

다음으로 필요한 건 카메라 공간에서 양의 x축을 나타낼 오른쪽 방향 벡터입니다. 오른쪽 방향 벡터를 얻으려면 먼저 (월드 공간에서) 위쪽을 가리키는 벡터를 정하고 약간의 트릭을 사용해야 합니다. 그런 다음 2 단계에서 얻은 벡터와 위쪽 벡터의 외적을 구합니다. 외적의 결과는 두 벡터에 수직인 벡터이므로 양의 x축을 가리키는 벡터를 얻습니다.

glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f); 
glm::vec3 cameraRight = glm::normalize(glm::cross(up, cameraDirection));

4. Up axis

이제 z축 벡터와 x축 벡터를 구했으니, 카메라의 양의 y축 벡터를 구하는 것은 간단합니다. 두 벡터의 외적을 구하기만 하면 됩니다.

glm::vec3 cameraUp = glm::cross(cameraDirection, cameraRight);

외적의 도움과 몇 가지 트릭을 써서 뷰/카메라 공간에 대한 모든 벡터를 구했습니다. 수학에 흥미가 있으신 독자분들을 위해 말씀드리자면, 이 과정은 선형 대수학에서 그람-슈미트 과정이라고 알려져 있습니다. 이제 저 카메라 벡터들을 이용해 카메라를 만드는데에 굉장히 유용한 LookAt 행렬을 만들 수 있습니다.

Look At

행렬의 멋진 점은 만약 당신이 3개의 수직(또는 비선형인)축을 사용해서 좌표 공간을 정의 할 때 해당 3개의 축과 변환 벡터를 사용하여 행렬을 만들 수 있고 이 행렬을 곱하는 것으로 어떤 벡터든 해당 좌표 공간으로 변환할 수 있다는 것입니다. 바로 이것이 LookAt 행렬이 하는 일이며 우리들도 카메라 공간을 정의하는 3개의 축과 위치 벡터를 갖고 있으므로 LookAt 행렬을 만들 수 있습니다.

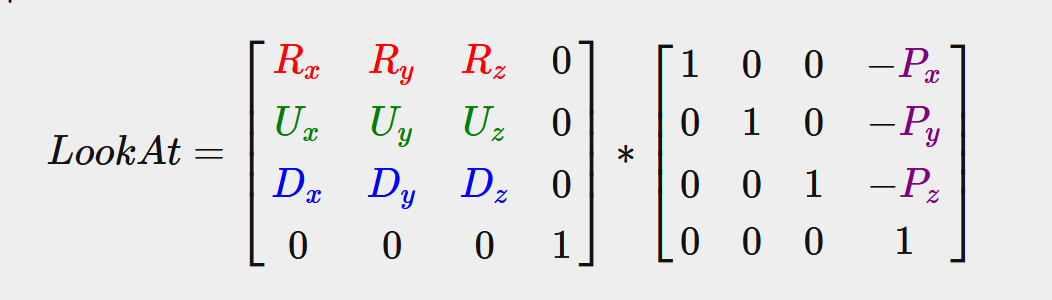
R은 오른쪽 벡터, U는 위쪽 벡터, D는 (카메라의)방향 벡터, 그리고 P는 카메라의 위치 벡터입니다. 알아두셔야 할 점은 회전(왼쪽 행렬)과 이동(오른쪽 행렬) 부분은 카메라가 이동하려는 방향의 반대 방향으로 월드를 회전시키고 이동시키는 것이기 때문에 반전(각각 전치 및 음수)되어야 한다는 것입니다. 이 LookAt 행렬을 사용하면 월드 좌표를 방금 우리가 정의한 뷰 공간으로 변환해주는 효과적으로 뷰 행렬로 쓸수 있습니다. LookAt 행렬은 말 그대로: 타겟을 보는 뷰 행렬을 만듭니다.

우리에겐 운 좋게도, GLM이 이런 작업들을 처리해줍니다. 우린 카메라 위치와 타겟의 위치, 월드 공간에서의 위쪽 벡터(오른쪽 벡터를 계산할 때 썼던 벡터)만 지정해 주면 됩니다. 그러면 GLM이 우리가 뷰 행렬로 쓸 LookAt 행렬을 만듭니다.

glm::mat4 view;
view = glm::lookAt(glm::vec3(0.0f, 0.0f, 3.0f), 
  		   glm::vec3(0.0f, 0.0f, 0.0f), 
  		   glm::vec3(0.0f, 1.0f, 0.0f));

glm::LookAt 함수는 위치, 타겟과 위쪽 벡터가 필요합니다. 이 예제는 지난 장에서 생성한 뷰 행렬과 같은 행렬을 생성합니다.

사용자 입력을 살펴보기 전에 씬을 회전하는 카메라를 만들어 봅시다. 타겟은 씬의 (0,0,0)에 두고, 삼각버을 사용하여 원의 한 점을 나타내는 각 프레임의 x 및 z 좌표를 만들고 이를 카메라 위치에 사용할 것입니다. 시간이 지남에 따라 x 및 y 좌표를 다시 계산하여 원의 모든 점을 가로지르므로 카메라가 장면을 중심으로 회전합니다. 우리는 이 원을 미리 정의된 방경만큼 확대하고 GLFW의 GLFWGetTime 함수를 사용하여 매 프레임마다 새로운 뷰 행렬을 생성합니다.

const float radius = 10.0f;
float camX = sin(glfwGetTime()) * radius;
float camZ = cos(glfwGetTime()) * radius;
glm::mat4 view;
view = glm::lookAt(glm::vec3(camX, 0.0, camZ), glm::vec3(0.0, 0.0, 0.0), glm::vec3(0.0, 1.0, 0.0));

코드를 작동시키면 이런 화면이 보일겁니다.

https://learnopengl.com/video/getting-started/camera_circle.mp4

이 작은 코드 조각으로 이제 카메라는 시간이 지남에 따라 씬 주위를 돌게 됩니다. 반경 및 위치/ 방향 매개변수를 자유롭게 실험하여 이 LookAt 행렬이 작동하는 방식을 느끼십시오. 또한 막힌 경우 소스 코드를  확인하십시오.

Walk around

씬을 돌아다니도록 카메라를 움직이는 것도 재밌지만 우리가 직접 움직이게 하는 건 더 재미있습니다! 먼저 카메라 시스템을 설정해야 합니다. 그러니 프로그램 상단에 몇 가지 카메라 변수를 정의하면 좋습니다.

glm::vec3 cameraPos   = glm::vec3(0.0f, 0.0f,  3.0f);
glm::vec3 cameraFront = glm::vec3(0.0f, 0.0f, -1.0f);
glm::vec3 cameraUp    = glm::vec3(0.0f, 1.0f,  0.0f);

이제 LookAt 함수는 이렇게 됩니다:

view = glm::lookAt(cameraPos, cameraPos + cameraFront, cameraUp);

먼저 카메라 위치를 전에 정의했던 cameraPos로 설정합니다. 방향은 현재 위치 + 방금 정의한 방향 벡터입니다. 이걸로 우리가 아무리 움직여도 카메라는 계속해서 타겟 방향을 보게됩니다. 일부 키를 누를 때 cameraPos 벡터를 업데이트하여 이러한 변수를 조금 사용해 보겠습니다.

GLFW의 키보드 입력을 관리하기 위해 이미 processInput 함수를 정의했으므로 몇가지 추가 키 명령을 추가해 보겠습니다.

void processInput(GLFWwindow *window)
{
    ...
    const float cameraSpeed = 0.05f; // adjust accordingly
    if (glfwGetKey(window, GLFW_KEY_W) == GLFW_PRESS)
        cameraPos += cameraSpeed * cameraFront;
    if (glfwGetKey(window, GLFW_KEY_S) == GLFW_PRESS)
        cameraPos -= cameraSpeed * cameraFront;
    if (glfwGetKey(window, GLFW_KEY_A) == GLFW_PRESS)
        cameraPos -= glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
    if (glfwGetKey(window, GLFW_KEY_D) == GLFW_PRESS)
        cameraPos += glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
}

WASD 키 중 하나를 누를 떄마다 카메라의 위치가 그에 따라 업데이트됩니다. 앞으로 또는 뒤로 이동 하려면 속도 값으로 조정된 위치 벡터에서 방향 벡터를 더하거나 뺍니다. 옆으로 이동하려면 외적을 수행하여 올바른 벡터를 만들고 그에 따라 오른쪽 벡터를 따라 이동합니다. 이것은 카메라를 사용할 때 익숙한 스트레이프 효과를 만듭니다.

결과값으로 나온 오른쪽 벡터를 정규화한다는 점을 알아두시길 바랍니다. 만약 결과값을 정규화하지 않으면 외적은 cameraFront 변수에 따라 다른 크기의 벡터를 반환할 수 있습니다. 이는 카메라 방향에 따라 이동속도가 느리거나 빨라질 수 있음을 의미합니다.

이미 카메라를 어느 정도 움직일 수 있을 겁니다. 시스템에 따른 속도이긴 하지만  cameraSpeed를 조정해야 할 수도 있습니다.

Movement speed

현재 우리는 이동속도로 상수 값을 쓰고 있습니다. 이론상으론 괜찮아 보이지만 실제로는 컴퓨터마다 처리 능력이 다르기 때문에 어떤 사람은 같은 시간 동안 다른 사람보다 훨씬 더 많은 프레임을 렌더링할 수도 있습니다. 사용자가 다른 사용자보다 더 많은 프레임을 렌더링할 때마다 그는 또한 processInput을 더 자주 호출합니다. 그 겨과 어떤 사람들은 설정에 따라 정말 빠르게 움직이고 어떤 사람들은 정말 느리게 움직입니다. 애플리케이션을 배포할 때 모든 종류의 하드웨어에서 동일하게 실행되는지 확인하고 싶습니다.

그래픽 애플리케이션과 게임은 일반적으로 마지막 프레임을 렌더링하는 데 걸린 시간을 저장하는 deltatime 변수를 추적합니다. 그런 다음 모든 속도에 이 deltaTime 값을 곱합니다. 결과는 프레임에 큰 deltaTime이 있을 때, 즉 마지막 프레임이 평균보다 오래 걸렸다는 것을 의미하며, 그 프레임의 속도도 이 모든 균형을 맞추기 위해 조금 더 높아집니다. 이 접근 방식을 사용할 때 PC가 매우 빠르든 느리든 상관없이 카메라의 속도는 그에 따라 균형을 이루므로 각 사용자가 동일한 경험을 할 수 있습니다.

deltaTime 값을 추적하기 위해 2개의 전역 변수가 필요합니다.

float deltaTime = 0.0f;	// Time between current frame and last frame
float lastFrame = 0.0f; // Time of last frame

그런다음 각 프레임 내에서 deltaTime 값을 계산합니다.

float currentFrame = glfwGetTime();
deltaTime = currentFrame - lastFrame;
lastFrame = currentFrame;

이제 deltaTime을 속도 계산할 때 사용할 수 있습니다.

void processInput(GLFWwindow *window)
{
    float cameraSpeed = 2.5f * deltaTime;
    [...]
}

delteTime을 사용하면 카메라가 초당 2.5unit의 고정된 속도로 움직입니다. 이전 섹션보다 더 부드럽고 일관적인 카메라 움직임을 볼 수 있습니다.

https://learnopengl.com/video/getting-started/camera_smooth.mp4

이제 우리는 모든 시스템에서 같은 속도로, 원하는 방향으로 움직이는 카메라를 가지게 되었습니다. 만약 진행하는 데에 어려움이 있다면 소스 코드를 확인해주세요. deltaTime은 이동과 관련되었을 때 자주 보게 될 것입니다.

Look around

오직 키보드만으로 움직이는 것은 그렇게 흥미롭진 않습니다. 특히 회전을 할 수 없는 건 움직임을 제한시킵니다. 바로 그럴 때, 마우스가 필요한 순간이죠!

씬 주변을 둘러보기 위해선 cameraFront 벡터를 마우스 입력에 따라 바꿔줘야 합니다. 하지만 마우스 회전에 따라 방향 벡터를 바꾸는 것은 다소 복잡하고 약간의 삼각법 지식을 필요로 합니다. 만약 삼각법에 대해 모르더라도 괜찮습니다. 코드 섹션까지 넘어가서 코드만 복붙하여 쓰고, 나중에 내용이 궁금해지면 언제든지 돌아와 다시 보면 됩니다.

Eule angles(오일러 각)

오일러 각은 3D에서 어떤 각이든 표현할 수 있는 3개의 값입니다. Leonhard Euler가 1700년대에 정의하였습니다. 오일러 각에는 3가지 요소가 있습니다: pitch, yaw, roll. 아래 이미지에서 직접 확인할 수 있습니다.

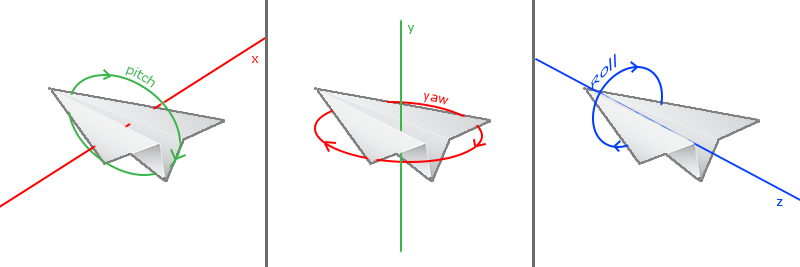
pitch 는 첫 번째 이미지와 같이 위 또는 아래를 얼마나 많이 보고 있는지를 나타내는 각도입니다. yaw는 왼쪽 또는 오른쪽을 보고 있는 각도를, roll은 우주 비행 카메라 처럼 몸통을 굴리는 것을 나타냅니다. 각각의 오일러 각은 단일 값으로 표시되며 3가지 모두의 조합으로 3D에서 모든 회전 벡터를 계산할 수 있습니다.

우리는 카메라 시스템에서 pitch와 yaw값만 쓸 것이므로 roll 값에 대해선 다루지 않겠습니다. pitch와 yaw값이 주어지면 그것들을 새로운 방향 벡터를 나타내는 3D 벡터로 변환할 수 있습니다. pitch와 yaw 값을 방향 벡터로 변환하는 프로세스에는 약간의 삼각법이 필요합니다. 기본적인 경우부터 시작합니다.

복습 먼저 해보겠습니다. 일반적인 직각 삼각형의 경우(한 쪽이 90도 각도인 경우)를 확인하겠습니다.

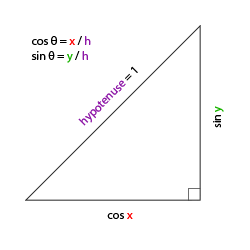
빗변의 길이를 1로 정의하면 삼각법(soh cag toa)을 통해 인접한 변의 길이가 cos x/h = cos x/1 = cos x이고 반대쪽의 길이가 sin y/h=sin y/1=sin y 임을 알 수 있습니다. 이 사실에서 각도에 따라 직각 삼각형의 x 및 y변의 길이를 구하는 일반식을 얻을 수 있습니다. 이를 이용하여 방향 벡터의 구성 요소를 계산해 보겠습니다.

머릿속에 삼각형 하나를 그려보세요. 이제 그 삼각형의 한 변을 x축에 평행하도록 하고 인접한 변은 y축에 평행하도록 그리고, (y축을 아래로 내려다보는 것처럼) 위쪽에서 살펴본다고 생각합시다.

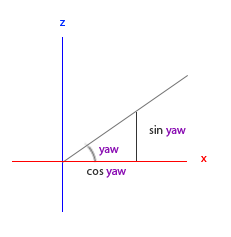
yaw 각도를 x측면에서 시작하여 반시게 방향 각도로 시각화하면 x측면의 길이가 cos(yaw)와 관련되어 있음을 알 수 있습니다. 그리고 비슷한 방식으로 z측면의 길이가 sin(yaw)와 관련되어 있음을 알 수 있습니다.

이 지식을 가지고 주어진 yaw 값을 취하면 카메라 방향 벡터를 만드는데 사용할 수 있습니다.

glm::vec3 direction;
direction.x = cos(glm::radians(yaw)); // Note that we convert the angle to radians first
direction.z = sin(glm::radians(yaw));

이것은 yaw 값에서 3D 방향 벡터를 얻는 방법을 해결하지만 피치도 포함해야 합니다. 이제 xz평면에 앉아 있는 것처럼 y축 측면을 살펴보겠습니다.

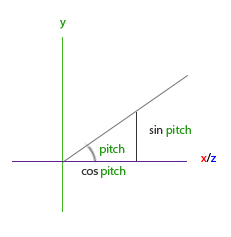
비슷하게 이 삼각형에서 우리는 방향의 y성분이 sin(pitch)와 같다는 것을 알 수 있으므로 그것을 채워봅시다.

direction.y = sin(glm::radians(pitch));

하지만 pitch 삼각형에서 xz측면도 cos(pitch)의 영향을 받는 것을 볼 수 있으므로 이것이 방향 벡터의 일부인지 확인해야 합니다. 이를 포함하면 yaw 및 pitch 오일러 각도에서 변호나된 최종 방향 벡터를 얻을 수 있습니다.

direction.x = cos(glm::radians(yaw)) * cos(glm::radians(pitch));
direction.y = sin(glm::radians(pitch));
direction.z = sin(glm::radians(yaw)) * cos(glm::radians(pitch));

이것이 우리에게 yaw 및 pitch 값 둘러보는 데 사용할 수 있는 3차원 방향 벡터로 변환하는 공식을 제공합니다.

모든 것이 음의 z축 방향으로 배치되도록 씬 월드를 설정했습니다. 그러나 x 및 z yaw 삼각형을 보면 θ가 0이면 카메라의 방향 벡터가 양의 x축을 가리키게 됨을 알 수 있습니다. 카메라가 기본적으로 음의 z축을 향하도록 하기 위해 yaw의 기본값을 시계 방향으로 90도 회전할 수 있습니다. 양수 각도는 시계 반대 방향으로 회전하므로 기본 yaw 값을 다음과 같이 설정합니다.

yaw = -90.0f;

아마 지금쯤이면 이런 궁금증이 생길 것입니다: yaw와 pitch 값은 어떻게 설정하고 수행하지?

참고: https://learnopengl.com/Getting-started/Camera