그래프

그래프

트리는 한 노드에서 다른 노드로 이동하는 경로가 하나만 존재하므로 순환적인 구조를 나타낼 수 없다. 순환적인 구조는 도로망이나 네트워크망 등 여러 곳에서 쓰이기 때문에 필요하며 이럴 땐 그래프 구조를 사용하는 것이 바람직하다.

그래프의 종류

에지에 가중치 정보를 저장하는지에 따라 비가중 그래프와 가중 그래프로 구분할 수 있다.

1. 비가중 그래프(unweighted graph): 노드에 다른 어떤 노드들이 연결되어 있는지에 대한 정보를 저장
   
2. 가중 그래프(weighted graph: 에지에 노드와 노드 사이의 거리를 저장, 도로망에서 특정 장소에서 다른 장소로 이동하는 최단 거리를 찾는 문제 등에서 사용
   

에지의 방향성에 따라 무방향 그래프와 방향 그래프로 나눌 수 있다.

1. 무방향 그래프(undirected graph): 에지가 양방향, 노드 A와 노드 B 사이를 양방향에서 이동할 수 있음
   
2. 방향 그래프(directed graph): 에지에 방향성이 있음, 만약 노드 A와 노드 B 사이를 움직일 수 있는 것을 표현하고 싶으면 노드 A에서 노드 B가는 에지와 노드 B에서 노드 A로 가는 에지를 따로 표현해야 함

인접 행렬로 그래프 표현

N 개의 노드를 가진 그래프는 N*N 크기의 2차원 배열로 표현할 수 있다. 이 배열에서 특정 원소는 해당 원소 인덱스에 해당하는 노드 사이의 가중치를 표현한다. 예를 들어 data[1][2]는 1번 노드와 2번 노드를 잇는 에지의 가중치를 나타냄. 이러한 방식으로 그래프를 표현하는 방벙을 인접 행렬(adjacency matrix)이라고 함.

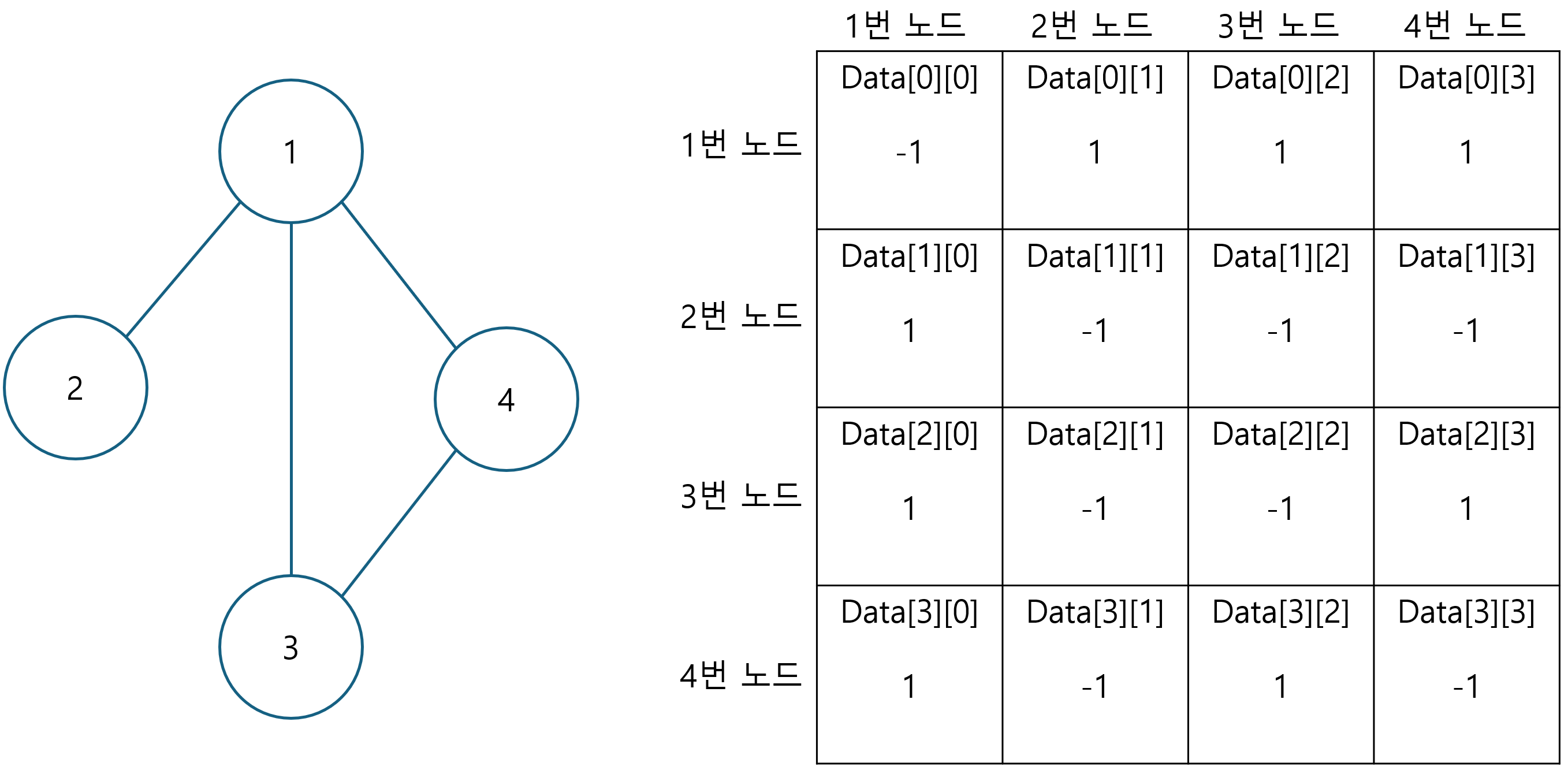
왼쪽 그래프의 연결 상태를 인접 행렬로 나타내면 오른쪽과 같다. 1번 노드는 자기 자신에게 연결되어 있지 않으니 data[0][0]는 0이 들어가고 1번 노드와 2번 노드는 연결되어 있지만 가중치가 없는 그래프 이므로 data[0][1]은 1이 들어간다.

행렬을 보면 뭔가 이상하지 않으가?

그렇다. 서로 연결되어 있지 않은 노드끼리의 정보도 -1을 넣어서 저장하고 있다.

인접 행렬로 표현된 그래프는 연결되지 않은 노드의 정보도 저장하기 때문에 메모리가 낭비 된다. 또한 한 노드에 연결된 다른 노드들을 알고 싶으면 data[a][0]부터 행렬의  크기인 n까지. 즉, data[a][n]까지 모두 방문해야 하므로 O(n)의 시간 복잡도를 가진다.

하지만 두 노드가 서로 연결되었는지를 알고 싶을 때는 data[a][b]에만 방문하면 되기 때문에 O(1)의 시간 복잡도를 가진다.

구현 코드

std::vector<std::vector<int>> data;

// 입력 받은 숫자만큼의 노드로 구성된 그래프를 구성하는 생성자
graph(int n)
{
    data.reserve(n);
    std::vector<int> row(n);
    std::fill(row.begin(), row.end(), -1);


    for (int i = 0; i < n; i++)
    {
        data.push_back(row);
    }
}

벡터 안에 벡터를 저장하는 식으로 구현하며, 노드의 개수를 입력 받아서 그 수의 크기만큼 행렬을 만들고 모두 -1을 채웁니다.

벡터말고 2차원 배열을 사용해서 더 간단하게 구현할 수 있지만 인접 행렬로된 그래프는 검색 등의 동작을 할 때 너무 큰 시간 복잡도를 가진다는 단점이 있다.

이러한 단점을 보완한 것이 인접 리스트로 표현한 그래프이다.

인접 리스트로 그래프 표현

추가 예정